Waves
Types of Waves
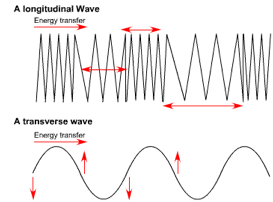
· Longitudinal waves are caused by a vibration that is parallel to the direction of the wave e.g. sound
· Transverse waves are caused by a vibration that is perpendicular to the direction of the wave e.g. electromagnetic waves, waves on a string

![]()
![]()
![]()
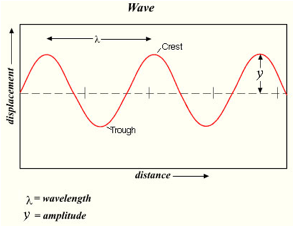
Properties of Waves
![]()
![]()

![]()
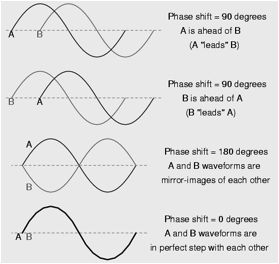
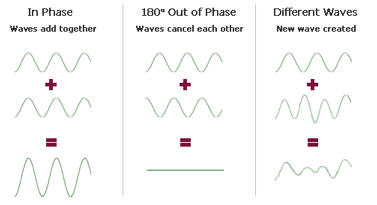
Phase
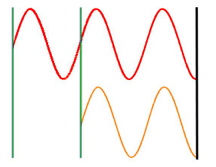
· Sometimes we also use the term ‘path difference’ to describe the difference between two waves
for example – the red wave here has travelled a distance of 1 wavelength or _ further than the orange wave – but they are still in phase (phase difference of 0 or 3600
· A path difference of _/2 would make 2 identical waves 180 out of phase
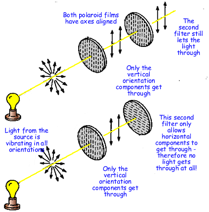
Polarisation
· Only transverse waves have polarisation
· It is a measure of the angle of vibration as viewed along the axis of the wave
· Unpolarised waves have all angles present
· A polaroid is a material that can polarise light in one angle
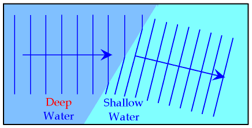
Wave Fronts
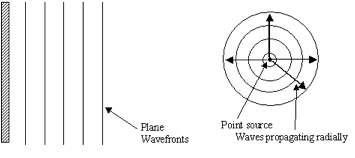 Waves produced by a ripple tank are called wave
fronts
Waves produced by a ripple tank are called wave
fronts
Each line represents the crest of a wave
The distance between two wave fronts in the wavelength
![]()
![]()
![]()
![]()
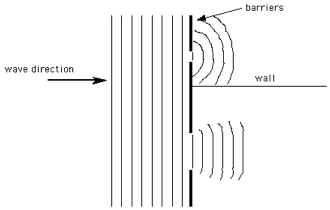
Superposition
· The principle of superposition is that when two waves meet, the total displacement at a point is equal to the sum of the individual displacements at that point
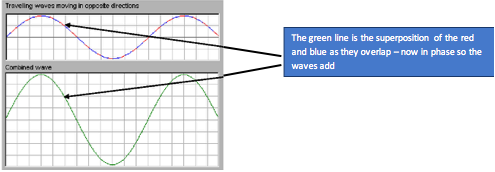
Stationary Waves
· A wave that moves through a medium and carries energy from one place to another is called a progressive wave
· A stationary wave (sometimes referred to as a ‘standing wave’)
- Does not transfer energy (it stores it)
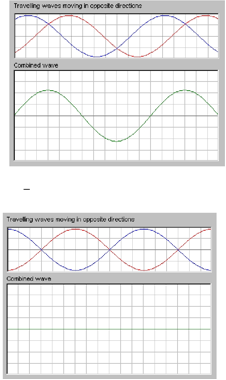
- Is formed when two progressive waves pass through each other in opposite directions
- When the waves have the same frequency/wavelength and similar amplitude
- Can be formed in many different places e.g. on a vibrating string, by sound in a tube, by microwaves reflecting from metal plates
- Only occur when the progressive waves have certain frequencies
Imagine two progressive waves of equal wavelength/frequency and the same amplitude meeting from opposite directions.:

![]()
![]()
![]()
![]()
![]()

![]()


 |
![]()
![]()

![]()
![]()
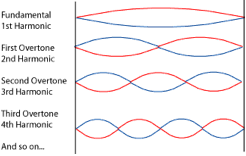
Using the wave equation and the wavelength of the wave compared to the length of the gap gives formula for the frequency of waves which will produce stationary waves:
![]()